반응형
동적 계획법(dynamic programming)은 복잡한 문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법을 뜻한다.
동적 계획법의 원리와 구현 방식
- 큰 문제를 작은 문제로 나눌 수 있어야 한다.
- 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들의 결과값은 항상 같아야한다.
- 모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하며 추후 재사용할 때는 DP 테이블을 이용한다. 이를 메모이제이션(memoization) 기법이라고 부른다.
- 동적 계획법은 톱-다운(top-down) 방식과 바텀-업(button-up) 방식으로 구현 할 수 있다.
피보나치 수열 공식 ex) 1, 1, 2, 3, 5
D[N] = D[N -1] + D[N - 2]
1. 동적 계획법으로 풀 수 있는지 확인하기
ex) 6번쨰 피보나치 = 5번째 피보나치 + 4번째 피보나치
2. 점화식 세우기
논리적으로 전체 문제를 나누고, 전체 문제와 부분 문제간의 인과 관계를 파악하는게 중요하다.
3. 메모이제이션 원리 이해하기
메모이제이션은 부분 문제를 풀었을 때 이 문제를 DP 테이블에 저장해 놓고 다음에 같은 문제가 나왔을 때 재계산하지 않고 DP 테이블의 값을 이용하는 것을 말한다.
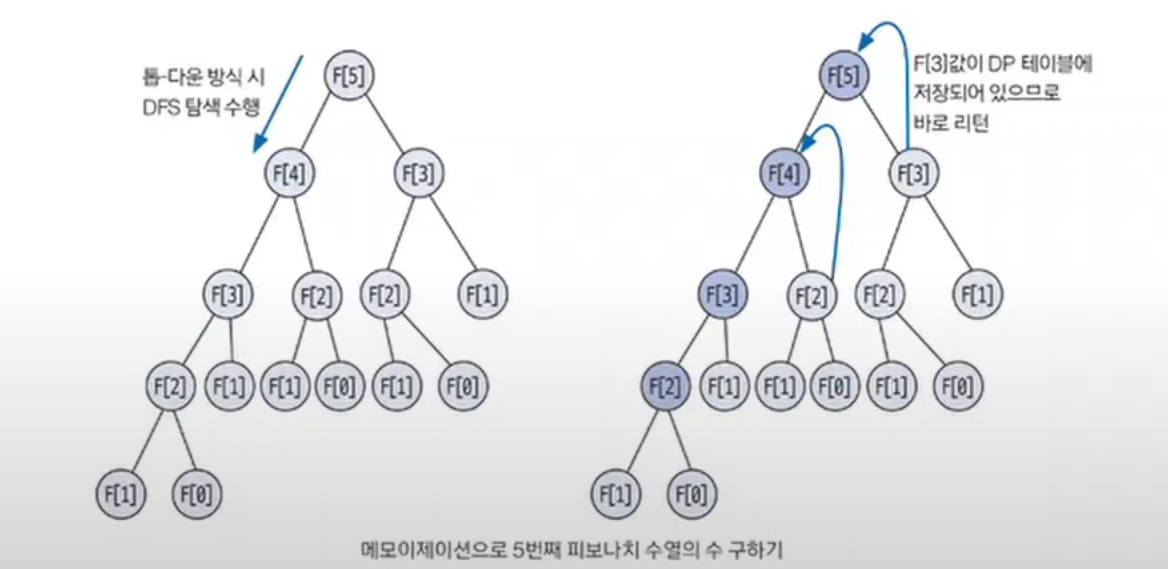
4. 톱-다운 구현 방식 이해하기
a. 위에서 문제를 파악해 내려오는 방식으로, 재귀 함수 형태로 코드 구현
코드의 가독성이 좋고, 이해하기가 쉽다.
#include<iostream>
using namespace std;
static int D[45];
int Fibo(int num) {
if (D[num] != -1) {
return D[num];
}
return D[num] = Fibo(num - 2) + Fibo(num - 1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
for (int i = 0; i <= n; i++) {
D[i] = -1;
}
D[0] = 0;
D[1] = 1;
Fibo(n);
cout << D[n];
}
5. 바텀-업 구현 방식
#include<iostream>
using namespace std;
static int D[45];
int Fibo(int num) {
if (D[num] != -1) {
return D[num];
}
return D[num] = Fibo(num - 2) + Fibo(num - 1);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
D[0] = 0;
D[1] = 1;
for (int i = 2; i <= n; i++) {
D[i] = D[i - 1] + D[i - 2];
}
Fibo(n);
cout << D[n];
}
바텀-업 방식이 더 안전한 방식으로, 톱-다운 방식은 재귀 함수의 형태로 구현되기 때문에 재귀의 깊이가 매우 깊어질 경우 런타임 에러가 발생할 수 있다.
본인에게 더 편한 방식을 찾아 선택해 사용하면 된다.
반응형
'알고리즘 > Do it! 알고리즘 코딩테스트 C++' 카테고리의 다른 글
| 섹션 8. 조합(Combination) (0) | 2023.04.03 |
|---|---|
| 섹션 7. 트리(Tree) (0) | 2023.04.02 |
| 섹션 6. 그래프(Graph) (1) | 2023.03.31 |
| 섹션 5. 정수론 (0) | 2023.03.30 |
| 섹션 4. 탐욕 알고리즘(Greedy Algorithm) (0) | 2023.03.29 |




댓글